Radical pair model
We consider radical pairs subject to coherent evolution under the local Hamiltonians of their constituent radicals and spin-selective recombination proceeding with the same rate constant, \(k_S=k_T=k\), for the singlet and triplet channel. Inter-radical interactions are neglected, as is spin relaxation. In this simplified, but commonly studied scenario17,25,26, the spin dynamics of the RP and its associated magnetic field effects (MFEs) can be described by the following master equation for the spin density operator \(\hat\rho (t)\):
$$\beginaligned \frac\mathrmd\hat\rho (t)\mathrmdt&= – i\left[ \hatH,\hat\rho (t) \right] – \frack_S2\left\{ \hatP_S,\hat\rho (t) \right\} – \frack_T2\left\{ \hatP_T,\hat\rho (t) \right\} \nonumber \\&= – i\left[ \hatH,\hat\rho (t) \right] – k\hat\rho (t), \endaligned$$
(1)
where [] and denote the commutator and anti-commutator, respectively. Here, the Hamiltonian is of the form \(\hatH = \hatH_\mathrmA + \hatH_\mathrmB\) with subscripts A and B referring to the two radicals, and \(\hatP_S\) and \(\hatP_T = \hat1 – \hatP_S\) are projection operators onto the singlet state and triplet manifold, respectively. The chemical reactivity has been included using the Haberkorn approach34, which gives rise to minimal singlet-triplet dephasing (alternative approaches have been suggested, but for \(k_S=k_T\) the differences of various master equation are lessened29,35). The Hamiltonians \(\hatH_i\), \(i \in \A, B\\), account for the Zeeman interactions between the electron spins and the applied magnetic field and the hyperfine interactions between the electron and nuclear spins within radical i (\(\hbar = 1\)):
$$\beginaligned {{\hatH}_\mathrmi} = \sum \limits _j {{{\hat\mathbfS}_i} \cdot \mathbfA_i,j \cdot {{{{\hat\mathbfI}}}_i,j}} + \vec \omega _i \cdot {{{{{\hat\mathbfS}}}}_i}. \endaligned$$
(2)
Here, the Larmor precession angular frequency is given by \(\vec \omega _i = -\gamma _i\vec B\), with \(\gamma _i\) denoting the gyromagnetic ratio of the electron in radical i and \(\vec B\) the applied magnetic field. \(\mathbf A_i, j\) is the hyperfine coupling tensor between the jth nuclear spin and the ith electron spin; \(\hat\mathbf I_i,j\) and \(\hat\mathbf S_i\) are the corresponding vector operators of nuclear and electron spin angular momentum.
Here, we solve Eq. (1) for realistically complex spin systems based on an approach employing spin correlation tensors (see Methods for details)25,36,37, to yield the quantum yield of recombination via the singlet channel, \(Y_S(\vartheta ,\varphi )\). Its sensitivity to changes in the applied magnetic field direction determine the compass fidelity, which we here assess in terms of established measures, namely the absolute anisotropy defined as
$$\beginaligned \Delta _S = \max _\vartheta , \varphi Y_S(\vartheta ,\varphi )-\min _\vartheta , \varphi Y_S(\vartheta ,\varphi ), \endaligned$$
(3)
where the polar angle \(\vartheta\) and azimuthal angle \(\varphi\) parametrize the direction of the applied magnetic field in the protein frame. We will relate this sensitivity measure to quantifiers of the quantum coherence present in the radical pair during its magnetosensitive spin evolution.
Measures of coherence
Various measures to quantify coherence have been developed11,12,13. Several such measures have previously been used in the context of the avian compass28,29,32,38,39. One canonical measure to quantify coherence is the relative entropy of coherence, which, in terms of the normalized density operator \(\hat\rho \) and a chosen basis, \(\\vert n \rangle \_n=1^d\), of the d-dimensional Hilbert space, is defined as
$$\beginaligned \mathcal C_r[\hat\rho ]=S[\mathbb I\mathbb C(\hat\rho )] – S[\hat\rho ], \endaligned$$
(4)
where \(S[\hat\rho ] = – \mathrm Tr[\hat\rho \log (\hat\rho )]\) is the von Neumann entropy and \(\mathbb I\mathbb C\) denotes the dephasing operation \(\mathbb I\mathbb C(\hat\rho ) = \sum _n \vert n \rangle \langle n \vert \hat\rho \vert n \rangle \langle n \vert\), which maps any quantum state into an incoherent state in the chosen basis.
Another measure, the \(l_1\)-norm of coherence11 is defined as
$$\beginaligned \mathcal C_l_1[\hat\rho ] = \sum _n\ne m \vert \langle n \vert \hat\rho \vert m \rangle \vert . \endaligned$$
(5)
Furthermore, we employ an additional measure suggested by Kominis defined by
$$\beginaligned \mathcal C_st[\hat\rho ] = S[\hatP_S\hat\rho \hatP_S+\hatP_T\hat\rho \hatP_T] – S[\hat\rho ], \endaligned$$
(6)
which reports singlet-triplet coherence while being independent of basis and unaffected by the degree of triplet coherence, which the author suggests was superior in assessing coherence in the radical pair-based compass29. Similarly, an alternative \(l_1\)-based measure of singlet-triplet coherence was used in ref. 40. The relative entropy of \(\hat\rho \) with respect to the maximally mixed state, \(S\left[ \hat1/d \right] = \log d – S\left[ \hat\rho \right]\), has likewise been employed to quantify the amount of basis-independent coherence31. Several alternative measures have been discussed in the literature29,31,40. We provide a comprehensive collection of results for these alternatives in the Supporting Information (SI), but focus on the above-mentioned measures in the main text for conciseness.
The coherence quantifiers introduced above can be employed to the entire density operator, \(\hat\rho \), as well as to the electronic part, \(\hat\sigma \), and are either basis-independent or defined with respect to a basis. In the present study, two clear choices include the singlet-triplet basis and the up-down basis of the electronic subspace, both of which will be used to evaluate \(\mathcal C_r\) and \(\mathcal C_l_1\) below. To distinguish these choices, we will henceforth index the coherence labels with \(\mathcal G\) (global, based on \(\hat\rho \)), \(\mathcal E\) (electronic, based on \(\hat\sigma \)), and ST (singlet-triplet basis) and UD (up-down basis). For example, \(\mathcal C_r^\mathcal E,U\!D\) corresponds to the electronic coherence assessed via the relative entropy quantifier in the up-down basis, which is the measure used by Jain et al.32. Note that, for all definitions used above, the non-trace preserving density matrix characteristic of recombining radical pair systems must be renormalized (by \(\mathrm Tr[\hat\rho ]\); which here simply yields the \(k=0\) result). As the coherence measures \(\mathcal C_i(t)\), \(i \in \ r, l_1, st \\), are time-dependent we further introduce the coherence yield as the time-averaged coherence measure weighted by the exponential decay kinetics of the radical pair:
$$\beginaligned \bar\mathcal C_i = k \int _0^\infty \mathcal C_i(t)\exp (-kt)\, \mathrm dt. \endaligned$$
(7)
For comparison to the anisotropy, we further define measures accounting for the variation of \(\bar\mathcal C_i\) with the magnetic field direction as
$$\beginaligned \mu [\bar\mathcal C_i]&= \frac \bar\mathcal C_i(\hat\rho _\max ) + \bar\mathcal C_i(\hat\rho _\min )2, \endaligned$$
(8)
and
$$\beginaligned \Delta [\bar\mathcal C_i]&= \bar\mathcal C_i(\hat\rho _\max ) -\bar\mathcal C_i(\hat\rho _\min ), \endaligned$$
(9)
where \(\hat\rho _\max \) and \(\hat\rho _\min \) corresponds to the density matrix associated with maximum and minimum singlet yield over magnetic field orientations. Furthermore, a field-independent measure is introduced as \([\bar\mathcal C_i]_B=0\), which is evaluated for \(B=0\).
Cai and Plenio have suggested an alternative, operational global quantifier of coherence28 in the context of a chemical compass in terms of the field-independent (\(B=0\)) singlet recombination yield due to the coherent part of the initial density operator \(\mathbb G\mathbb C(\hat\rho (0))\), with \(\mathbb G\mathbb C(\hat\rho ) = \hat\rho – \mathbb I\mathbb C(\hat\rho )\) evaluated in the eigenbasis of the hyperfine Hamiltonian:
$$\beginaligned [\mathcal C_y^\mathcal G]_B=0 = \Big \vert Y_S\Big (\hat\rho (0) = \mathrm Tr[\hatP_S]^-1\mathbb G {\mathbb C}(\hatP_S);B=0\Big )\Big \vert . \endaligned$$
(10)
In this paper we utilise both this measure and a generalised field-dependent version (with the magnetic field in the extremal directions) to allow us to also evaluate \(\mu [\mathcal C_y^\mathcal G]\) and \(\Delta [\mathcal C_y^\mathcal G]\).
Large spin system electronic coherence
Previous studies on coherence in the avian compass typically use systems with a modest number of nuclear spins (only one or 5–6) and often randomly assumed hyperfine interactions28,29,32,38,41. Under the assumptions as laid out above, we have been able to overcome this limitation and evaluate fidelities and coherence measures for flavin–tryptophan and flavin–tyrosine radical pairs with up to 21 nuclear spins and judiciously chosen hyperfine parameters, as summarized in the SI. Our implementation relied on GPU computing realized using CUDA, which vastly outperformed the corresponding calculations on CPUs. We have varied the relative orientation of the radicals, as parametrized by Euler angles, \(\alpha\), \(\beta\) and \(\gamma\), defining the orientation of the flavin radical relative to the radical partner. Using an angular resolution of 3 degrees, we have probed 878,400 relative orientations for each combination of radicals. For each radical orientation, we sampled 10,242 orientations of \(\vartheta\) and \(\varphi\) (5121 unique directions) to evaluate the fidelity measure \(\Delta _S\) and several associated coherence measures as introduced above. In what follows, we focus on the compass anisotropy \(\Delta _S\) and the coherence measures \(\mu [\bar\mathcal C_i]\) and \(\Delta [\bar\mathcal C_i]\), for both the ST and UD basis, and the \(l_1\)– and relative entropy of coherence quantifiers. Alternative measures are discussed in the SI, whereby qualitatively corresponding conclusions emerged. For all simulations, a magnetic field strength of 50 \(\mu\)T (comparable to the geomagnetic field in Northern Europe) and a radical lifetime of \(k^-1=1\mu\)s were assumed. The latter is in line with the order-of-magnitude lifetime of the magnetosensitive radical pairs in cryptochromes as observed for in vitro studies14,21 and the anticipated spin relaxation times20. Results for larger magnetic field strength may be found in the SI; these show increased anisotropy but reduced correlation with coherence measures (Figs. S1 and S2).
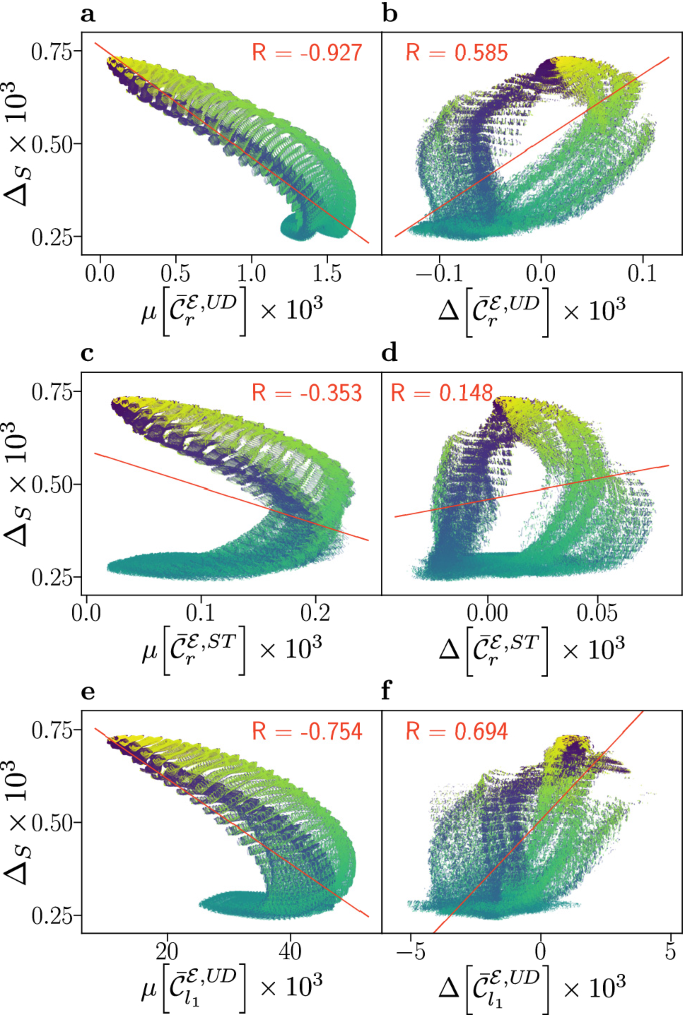
Compass sensitivity, as captured by the anisotropy \(\Delta _S\), is plotted against electronic coherence measures \(\mu [\bar\mathcal C_i]\) (a, c, e) and \(\Delta [\bar\mathcal C_i]\) (b, d, f), for 878,400 relative orientations of flavin–tryptophan radical pairs. The anisotropy \(\Delta _S\) quantifies the maximal change in the recombination quantum yield as the direction of the applied magnetic field is varied in the frame of the cryptochrome protein, with larger values corresponding to greater sensitivity. Here, we use the recombination weighted relative entropy of coherence \(\bar\mathcal C_r\) defined in Eq. (4), and the \(l_1\)-norm measure \(\bar\mathcal C_l_1\) defined in Eq. (5) evaluated in the Zeeman basis, also known as the “up-down” (UD) basis, and the singlet-triplet (ST) basis. Coherence is assessed by its mean value \(\mu [\bar\mathcal C_i]\) as defined in Eq. (8), and difference \(\Delta [\bar\mathcal C_i]\) as defined in Eq. (9), with respect to the magnetic field directions associated with maximal and minimal recombination yield. Alternative measures are covered in the Supporting Information. Data has been coloured according to the relative orientation angle \(\beta\), ranging from 0° (blue) to 180° (yellow) and a linear fit (red line) with associated Pearson correlation coefficient R is displayed.
For flavin–tryptophan systems the results are presented in Fig. 2, which shows plots of the absolute anisotropy vs. various electronic coherence measures. The absolute anisotropy \(\Delta _S\) measures the maximal spread of the quantum yield of radical pair recombination as the direction of the geomagnetic field is varied relative to the sensory protein. Thus, \(\Delta _S\) indicates the contrast of the sensor via a relative difference in reaction products with respect to magnetic field orientation and is widely accepted as a measure of compass sensitivity. In this way, Fig. 2 correlates this measure of compass sensitivity with measures quantifying the electronic coherence present during the lifetime of the radical pair. The data reveals diverse, i.e., not universal, and complex relations of fidelity and coherence measures. Surprisingly, an anti-correlation with respect to \(\mu [\bar\mathcal C_i]\) is observed that is present in both the UD and ST basis, but larger in the former. Specifically, \(\Delta _S\) is found to anti-correlate with \(\mu [\bar\mathcal C_r^\mathcal E, U\!D]\), which is based on the same coherence measure as used by Jain et al.32, giving rise to a remarkable correlation coefficient of \(R=-0.927\). In contrast, a positive (but weaker) correlation is observed with respect to the \(\Delta [\bar\mathcal C_r^\mathcal E,UD]\) measure. Similar results, shown in the SI, are found for correlations involving the relative anisotropy \(\Gamma _S\) (Fig. S3), which is a measure of compass sensitivity \(\Delta _S\) relative to the mean recombination yield.
Furthermore, the results show structured subsets of the data that may present positive or negative correlations. In our data discussed below, and in comparable studies in the literature, such structures in the correlation data appear to be absent for a small number of nuclear spins. This suggests that for comprehensive considerations of coherence in biology, systems must be sufficiently and realistically complex.
In the case of \(\Delta [\bar\mathcal C_r^\mathcal E,ST]\), the colouration of the plot according to the angle \(\beta\) demonstrates a relationship to the bands in which small values of \(\beta\) correspond to a stronger positive correlation (see Fig. 2d). However, maximal anisotropy is realized for \(\Delta [\bar\mathcal C_r^\mathcal E,ST] \approx 0\), a condition which appears to likewise approximately hold for the other coherence anisotropy measures used (see Fig. 2b,f). The implication is that, for this system, maximal compass sensitivity is not realized by minimizing electronic coherence in one extremal direction while maximizing it in the other, a strategy which, at least a priori, might have appeared auspicious in maximizing yield differences and thus compass fidelity.
Results for flavin–tyrosine radical pairs are shown in Fig. 3, in which smaller correlations are found than for the flavin–tryptophan model. An anti-correlation is still observed for \(\mu [\bar\mathcal C_r^\mathcal E,ST]\) and \(\Delta _S\), and likewise the weaker positive correlation persists between \(\Delta [\bar\mathcal C_r^\mathcal E,ST]\) and \(\Delta _S\). As in the flavin–tryptophan models, subsets of the data present positive and negative correlation. However, the structure of these subsets, and relationship to the angle \(\beta\) is different. Here, for mid-range values of \(\beta\), which correspond to maximal compass sensitivity, the results suggest a marked anti-correlation in \(\mu [\bar\mathcal C_r^\mathcal E,ST]\) and a strong positive correlation in \(\Delta [\bar\mathcal C_r^\mathcal E,ST]\). Similar results, shown in the SI (Figs. S3 and S4), are found for correlations involving the relative anisotropy \(\Gamma _S\).
The results on large spin systems are unexpected in view of previous studies17,29,38,42 and thought provoking with respect to Jain et al.’s suggestion of a compass operating in a regime of low coherence32. Here, our results based on the same coherence measure as used Jain et al. (\(\bar\mathcal C_r^\mathcal E, U\!D\)), appear to not only corroborate this conclusion, but lead to the supposition that the lack of electronic coherence is advantageous. This could imply an incoherent, relaxation-driven16,43 character of the avian compass.
Small spin system electronic and global coherence
We note that the coherence measures employed above, including \(\mathcal C_r^\mathcal E,U\!D\) as used by Jain et al., have not previously been assessed with respect to their principal predictive power of compass performance. We have thus systematically explored the correlation of compass fidelity and the various coherence measures employed, both for systems of reference-probe topology26,27 (with all hyperfine interactions confined to one radical) and systems with more symmetrically distributed hyperfine interactions, and for radical pair lifetimes of \(k^-1=1 \, \upmu\)s and \(k^-1=10 \, \upmu\)s. Details of this exploration are provided in the SI (Figs. S5–S8). In brief, we again find that there is significant variation of correlations for different systems and measures, overall supporting the view that electronic coherence is not the most effective predictor of compass sensitivity. In particular systems that combine the hyperfine interactions of N5 and N10 in flavin with random hyperfine couplings in the other radical exhibit low correlation between anisotropy and electronic coherence. However, as was the case in the study presented by Cai and Plenio28, a stronger correlation is found with global coherence measures, in particular \(\mathcal C^\mathcal G_y\). This measure corresponds to the coherent contribution to the singlet yield, and its broad success suggests that it is important that the global coherence quantifier relates to operation. Further measures and correlation plots supporting these findings can be found in the SI (Figs. S5–S8).
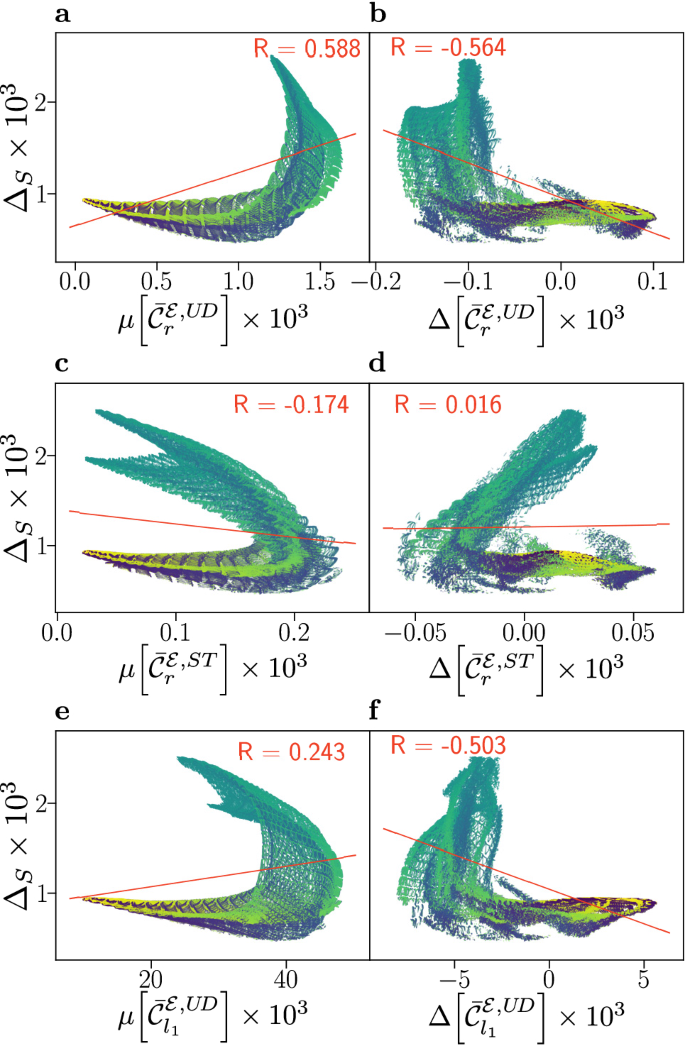
Compass sensitivity, as captured by the anisotropy \(\Delta _S\), is plotted against electronic coherence measures \(\mu [\bar\mathcal C_i]\) (a, c, e) and \(\Delta [\bar\mathcal C_i]\) (b, d, f), for 878,400 relative orientations of flavin–tyrosine radical pairs. Here, we use equivalent measures to Fig. 2, where additional details are provided; alternative measures are detailed in the SI. Data has been coloured according to the relative orientation angle \(\beta\), ranging from \(0^\circ \) (blue) to \(180^\circ \) (yellow). Both up-down (UD) and singlet-triplet (ST) bases are considered, and a linear fit (red line) with associated Pearson correlation coefficient R is displayed.
Large spin system global coherence
The confirmed applicability of \([\mathcal C_y^\mathcal G]_B=0\) motivated us to attempt a reassessment of the coherence-fidelity correlation of the large spin systems based on this global coherence measure. While global coherence measures are in general prohibitively expensive to evaluate for spin systems of the relevant size, \([\mathcal C_y^\mathcal G]_B=0\) can be approximated with reasonable effort from the analytical expression for the singlet yield (Eq. (S14) in the SI; implemented for graphics processing unit using CUDA). Using Monte Carlo sampling of the matrix elements of the singlet projection operator in the eigenbasis of the combined Hilbert space of both radicals assists in accelerating the calculation (see SI). Utilising this we have been able to evaluate \([\mathcal C_y^\mathcal G]_B=0\) of the flavin–tryptophan and flavin–tyrosine systems for a representative number of relative orientations.
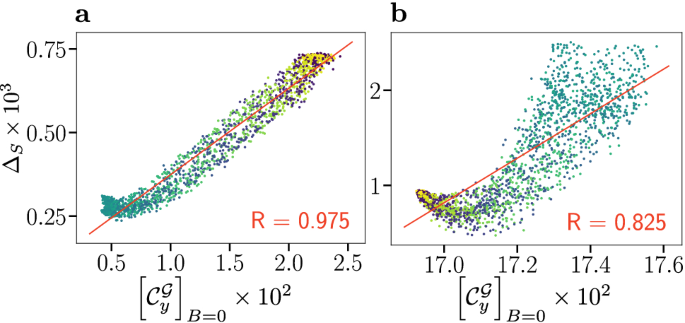
Compass anisotropy \(\Delta _S\) as a measure of compass sensitivity is plotted against the global measure of coherence \([\mathcal C_y^\mathcal G]_B=0\), an operational measure that represents the coherence contribution of the total nuclear and electronic state to the singlet yield evaluated in the absence of a magnetic field. (a) Correlation plot for the flavin–tryptophan model. (b) Correlation plot for flavin–tyrosine model. Data has been coloured according to the radical relative orientation angle \(\beta\), ranging from \(0^\circ \) (blue) to \(180^\circ \) (yellow), and a linear fit (red line) with associated Pearson correlation coefficient R is displayed.
In Fig. 4 we plot compass anisotropy \(\Delta _S\) of these systems as a function of global coherence \([\mathcal C_y^\mathcal G]_B=0\). For both systems, a strong positive correlation of \([\mathcal C_y^{{\mathcal G}}]_B=0\) and \(\Delta _S\) is found, thereby reinforcing the results for 5-6 nuclear spins, as studied previously28 and above. Specifically, we find a remarkable correlation for flavin–tryptophan for which \(R = +0.975\) based on 1784 randomly chosen relative orientations, in stark contrast to the anti-correlation of \(R = -0.927\) found with the electronic coherence measure \(\mu [\bar{{\mathcal C}}_r^\mathcal E,U\!D]\). The results for flavin–tyrosine are more structured, but likewise give rise to a strong overall correlation with \(R = +0.825\). This result confirms the supposition of Cai and Plenio, who proposed that global system-environment coherence is crucial for the compass sensitivity, based on simpler model systems28. Alongside our other results, this implies that the total system cannot be reduced to consideration of electronic subsystems. Nuclear coherences and nuclear-electronic coherences are an integral part of the processes.





More Stories
Three Keys of Branding That Will Turn Small Business Advertising Expense into an Investment
Perbedaan Logo Design Dengan Branding
Travel Agents Can Help With Vacations and Business Travel