Strategy stability analysis of each participant
In evolutionary game, three players dynamically adjust their strategies by adjusting the values of \(x\), \(y\) and \(z\), and optimize their strategies through learning and imitation. Evolutionary stable strategy (ESS) points must be robust to minor disturbances according to the stability theorem of differential equations and the properties of ESS36. In order to clarify the strategic choice of each participant, the dynamic evolution trend of three players is analyzed respectively, therefore, the critical condition for decision-making is identified.
Strategy stability analysis of private companies
The probability that private companies choose strategy P1 is \(x\). According to Eq. (4), the first derivative of \(F(x)\) is as follows:
$$\fracdF(x)dx = (1 – 2x)\left[ u_C (\omega L_P1 – L_P1 ) + \pi (y)\pi (z)u_C (F + E_p ) + \pi (y)\pi (1 – z)u_C (S_P ) \right]$$
(7)
When \(\pi (y) = \pi (y)* = \fracu_C (L_P1 – \omega L_P1 )\pi (z)u_C (F + E_p ) + \pi (1 – z)u_C (S_P )\), then \(\fracdF(x)dx \equiv 0\). It indicates that all strategies of private companies are at a steady state. Otherwise, when \(\pi (y) \ne \pi (y)*\), if under the condition that \(\pi (y) < \pi (y)*\), the results come as follows: \(\fracdF(x)dx|_x = 0 < 0\), \(\fracdF(x)dx|_x = 1 > 0\). In this case, it indicates that \(x = 0\) is ESS and private companies tend to choose strategy P2. If under the condition that \(\pi (y) > \pi (y)*\), then, \(\fracdF(x)dx|_x = 0 > 0\), \(\fracdF(x)dx|_x = 1 < 0\). In this case, it implies that \(x = 1\) is ESS and private companies prefer to choose strategy P1. Therefore, the response function of the probability \(x\) that private companies choose hardworking behavior strategy P1 is as follows:
$$x = \left\{ {\beginarray*20l 0, \hfill & if\;\pi (y) < \fracu_C (L_P1 – \omega L_P1 )\pi (z)u_C (F + E_p ) + \pi (1 – z)u_C (S_P ) \hfill \\ [0,1], \hfill & if\;\pi (y) = \fracu_C (L_P1 – \omega L_P1 )\pi (z)u_C (F + E_p ) + \pi (1 – z)u_C (S_P ) \hfill \\ 1, \hfill & {if\;\pi (y) > \frac{u_C (L_P1 – \omega L_P1 )}{\pi (z)u_C (F + E_p ) + \pi (1 – z)u_C (S_P )}} \hfill \\ \endarray } \right.$$
(8)
The dynamic phase diagram of private company is accordingly shown in Fig. 9. As shown above, the evolutionary equilibrium state of private companies is closely related to the strategy choice of citizens and the government. Along with the increase in the probability of citizens participation in regulation, the probability of private companies adopting effortful behavior strategy P1 increases and gradually converges to 1. Further analysis of the model shows that, in order to drive private companies to choose the P1 strategy, increasing the perceived value of government penalty \(u_C (F)\) and reputation loss \(u_C (S_P )\) is an effective method.
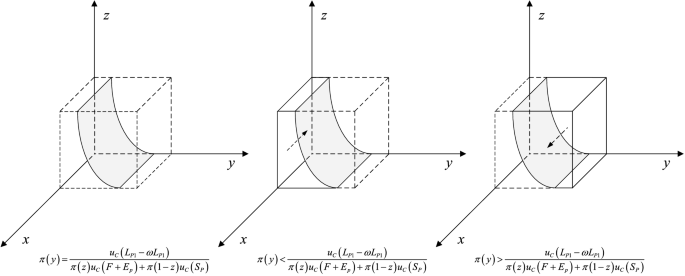
Replicated dynamic phase diagram of private company.
Strategy stability analysis of citizens
The probability that citizens choose strategy C1 is \(y\). According to Eq. (5), the first derivative of \(F(y)\) is as follows:
$$\fracdF(y)dy = (1 – 2y)\left[ – u_C (C_C1 ) + \pi (1 – x)\pi (z)u_I (E_G + E_p ) \right]$$
(9)
When \(\pi (z) = \pi (z)* = \fracu_C (C_C1 )\pi (1 – x)u_I (E_G + E_p )\), then \(\fracdF(y)dy \equiv 0\). It implies that all strategies of citizens are at a steady state. Otherwise, when \(\pi (z) \ne \pi (z)*\), if under the condition that \(\pi (z) < \pi (z)*\), the results come as follows: \(\fracdF(y)dy|_y = 0 < 0\), \(\fracdF(y)dy|_y = 1 > 0\). In this case, it represents that \(y = 0\) is ESS and citizens prefer to choose strategy C2. If under the condition that \(\pi (z) > \pi (z)*\), then, \(\fracdF(y)dy|_y = 0 > 0\), \(\fracdF(y)dy|_y = 1 < 0\). In this case, it implies that \(y = 1\) is ESS and citizens incline to choose strategy C1. Therefore, the response function of the probability \(y\) that citizens choose to impose supervision strategy C1 is as follows:
$$y = \left\{ {\beginarray*20l 0 \hfill & if\;\pi (z) < \fracu_C (C_C1 )\pi (1 – x)u_I (E_G + E_p ) \hfill \\ [0,1] \hfill & if\;\pi (z) = \fracu_C (C_C1 )\pi (1 – x)u_I (E_G + E_p ) \hfill \\ 1 \hfill & {if\;\pi (z) > \frac{u_C (C_C1 )}{\pi (1 – x)u_I (E_G + E_p )}} \hfill \\ \endarray } \right.$$
(10)
The dynamic phase diagram of citizen is accordingly shown in Fig. 10. The evolutionary equilibrium of citizens is closely related to the strategic choice of private companies and the government. With the increase of the probability of strict government supervision, the probability of strategy C1 that citizens participate in supervision increases and converges to 1. In addition, it is an effective way to increase the perceived value of compensation \(u_I (E_G )\) and \(u_I (E_P )\) to motivate the public to participate in supervision.
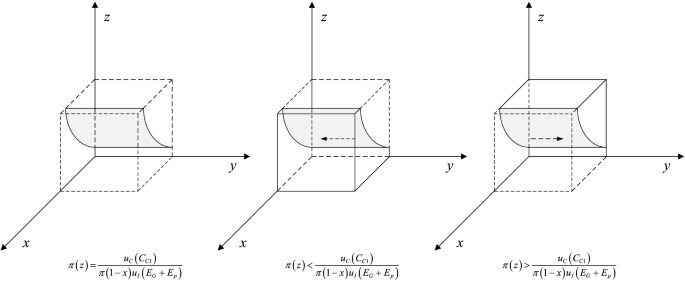
Replicated dynamic phase diagram of citizen.
Strategy stability analysis of the government
The probability that the government chooses strategy G1 is \(z\). According to Eq. (6), the first derivative of \(F(z)\) is as follows:
$$\fracdF(z)dz = (1 – 2z)\left[ u_I (G_G1 – G_G2 ) + \pi (y)\left[ – u_C (C_G ) + \pi (1 – x)\left[ u_I (F) + u_C (S_G – E_G ) \right] \right] \right]$$
(11)
When \(\pi (x) = \pi (x)* = \frac\pi (y)\left[ u_I (F) + u_C (S_G – C_G – E_G ) \right] + u_I (G_G1 – G_G2 )\pi (y)\left[ u_I (F) + u_C (S_G – E_G ) \right]\), then \(\fracdF(z)dz \equiv 0\). It implies that all strategies of the government are at a steady state. Otherwise, when \(\pi (x) \ne \pi (x)*\), if under the condition that \(\pi (x) < \pi (x)*\), the results come as follows: \(\fracdF(z)dz|_z = 0 > 0\), \(\fracdF(z)dz|_z = 1 < 0\). In this case, it represents that \(z = 1\) is ESS and the government tends to choose strategy G1 to implement strict regulation. If under the condition that \(\pi (x) > \pi (x)*\), then, \(\fracdF(z)dz|_z = 0 < 0\), \(\fracdF(z)dz|_z = 1 > 0\). In this case, it implies that \(z = 0\) is ESS and the government inclines to choose strategy G2. Therefore, the response function of the probability \(z\) that the government select strict supervision strategy G1 is as follows:
$$z = \left\{ {\beginarray*20l 0 \hfill & if\;\pi (x) > \frac\pi (y)\left[ u_I (F) + u_C (S_G – C_G – E_G ) \right] + u_I (G_G1 – G_G2 )\pi (y)\left[ u_I (F) + u_C (S_G – E_G ) \right] \hfill \\ [0,1] \hfill & {if\;\pi (x) = \frac\pi (y)\left[ u_I (F) + u_C (S_G – C_G – E_G ) \right] + u_I (G_G1 – G_G2 )\pi (y)\left[ u_I (F) + u_C (S_G – E_G ) \right]} \hfill \\ 1 \hfill & {if\;\pi (x) < \frac{{\pi (y)\left[ u_I (F) + u_C (S_G – C_G – E_G ) \right] + u_I (G_G1 – G_G2 )}}{{\pi (y)\left[ u_I (F) + u_C (S_G – E_G ) \right]}}} \hfill \\ \endarray } \right.$$
(12)
The dynamic phase diagram of the government is accordingly shown in Fig. 11. The evolutionary equilibrium state of the government is closely related to the strategic choices of private companies and citizens. Along with the increase of the probability of private companies choosing strategy P2, the probability of strict regulation strategy G1 that increases and converges to 1. Further analysis based on the response function reveals that increasing the perceived benefits under strict supervision can promote positive regulatory behavior.
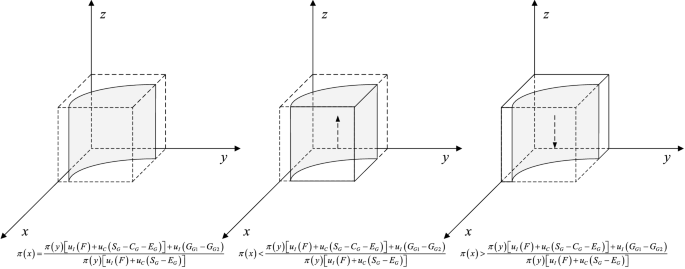
Replicated dynamic phase diagram of the government.
Strategy stability analysis of tripartite evolutionary game system
In combination with Eqs. (4), (5) and (6), a tripartite evolutionary dynamic system is obtained as follows:
$$\left\{ {\beginarray*20l F(x) = \fracdxdt = x(1 – x)(V_P1 – V_P2 ) = 0 \hfill \\ F(y) = \fracdydt = y(1 – y)(V_C1 – V_C2 ) = 0 \hfill \\ F(z) = \fracdzdt = z(1 – z)(V_G1 – V_G2 ) = 0 \hfill \\ \endarray } \right.$$
(13)
Solving the equations, 8 pure strategy equilibrium points are obtained, as \(P_1 (0,0,0)\), \(P_2 (1,0,0)\), \(P_3 (0,1,0)\), \(P_4 (0,0,1)\), \(P_5 (1,1,0)\), \(P_6 (1,0,1)\), \(P_7 (0,1,1)\), \(P_8 (1,1,1)\). According to the Lyapunov stability theory, the equilibrium of the replicated dynamic system is stable only if the eigenvalues of the Jacobian have negative real parts33. Specifically, when the eigenvalues of the Jacobian matrix corresponding to an equilibrium point are negative, the equilibrium point is a local stable point. While at least one eigenvalue of the Jacobian matrix is positive, the point is an unstable point. The Jacobian matrix of the system (13) can be obtained as:
$$J = \left[ \begingathered J_11 J_12 J_13 \hfill \\ J_21 J_22 J_23 \hfill \\ J_31 J_32 J_33 \hfill \\ \endgathered \right]$$
(14)
$$\left\{ {\beginarray*20l J_11 = \frac\partial F(x)\partial x = (1 – 2x)\left[ u_L (\omega L_P1 – L_P1 ) + \pi (y)\pi (z)u_L (F + E_p ) + \pi (y)\pi (1 – z)u_L (S_P ) \right] \hfill \\ J_12 = \frac\partial F(x)\partial y = x(1 – x)\left[ \pi (z)u_L (F + E_p ) + \pi (1 – z)u_L (S_P ) \right] \hfill \\ J_13 = \frac\partial F(x)\partial z = x(1 – x)\left[ \pi (y)u_L (F + E_p ) – \pi (y)u_L (S_P ) \right] \hfill \\ J_21 = \frac\partial F(y)\partial x = y(1 – y)\left[ – \pi (z)u_G (E_G + E_p ) \right] \hfill \\ J_22 = \frac\partial F(y)\partial y = (1 – 2y)\left[ – u_L (C_C1 ) + \pi (1 – x)\pi (z)u_G (E_G + E_p ) \right] \hfill \\ J_23 = \frac\partial F(y)\partial z = y(1 – y)\left[ \pi (1 – x)u_G (E_G + E_p ) \right] \hfill \\ J_31 = \frac\partial F(z)\partial x = z(1 – z)\left[ – \pi (y)\left[ u_G (F) + u_L (S_G – E_G ) \right] \right] \hfill \\ J_32 = \frac\partial F(z)\partial y = z(1 – z)\left[ – u_L (C_G ) + \pi (1 – x)\left[ u_G (F) + u_L (S_G – E_G ) \right] \right] \hfill \\ {J_33 = \frac\partial F(z)\partial z = (1 – 2z)\left[ u_G (G_G1 – G_G2 ) + \pi (y)\left[ – u_L (C_G ) + \pi (1 – x)\left[ u_G (F) + u_L (S_G – E_G ) \right] \right] \right]} \hfill \\ \endarray } \right.$$
(15)
As shown in Table 3, since the cost of public supervision is greater than 0, that is, \(u_C (C_C1 ) > 0\), then it is found that eigenvalue \(\lambda_ 2 > 0\) of \(P_3 (0,1,0)\), \(P_5 (1,1,0)\) and \(P_8 (1,1,1)\). It is obvious that benefits obtained under strict government supervision are higher than that of loose supervision. Due to \(u_I (G_G1 – G_G2 ) > 0\), as a result eigenvalue \(\lambda_ 3 > 0\) in \(P_1 (0,0,0)\) and \(P_2 (1,0,0)\). As for eigenvalue \(\lambda_ 2\) of \(P_4 (0,0,1)\), the reward and compensation from reporting opportunistic behavior is greater than the cost. Then it can be found that \(u_I (E_G + E_p ) > u_C (C_C1 )\), thus, \(P_4 (0,0,1)\) is not an equilibrium point. For \(u_C (L_P1 – \omega L_P1 ) > 0\), therefore, the eigenvalue \(\lambda_ 1\) of \(P_6 (1,0,1)\) is larger than 0. Based on the actual situation, the penalties for opportunistic behavior in private companies outweigh the benefits, that is, \(u_C (F + E_p ) > u_C (L_P1 – \omega L_P1 )\). Then eigenvalue \(\lambda_ 1 > 0\) of \(P_7 (0,1,1)\). Therefore, there is no stable equilibrium point in the tripartite game model according to the reality background.





More Stories
Three Keys of Branding That Will Turn Small Business Advertising Expense into an Investment
Perbedaan Logo Design Dengan Branding
Travel Agents Can Help With Vacations and Business Travel